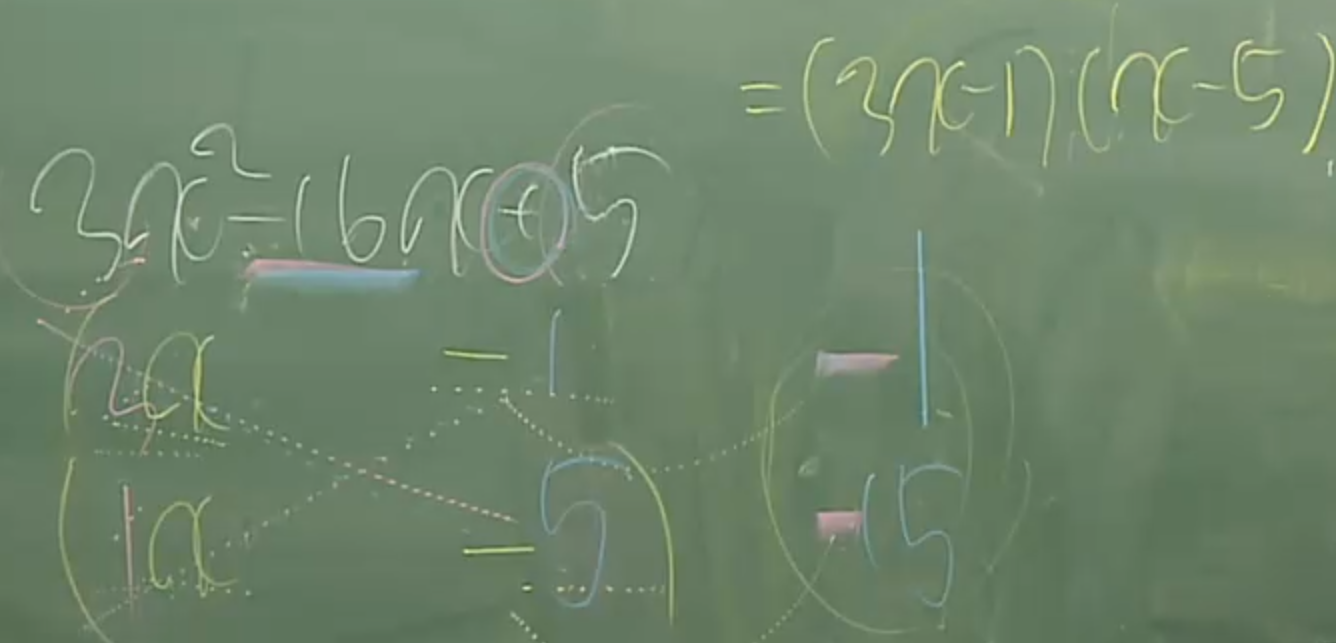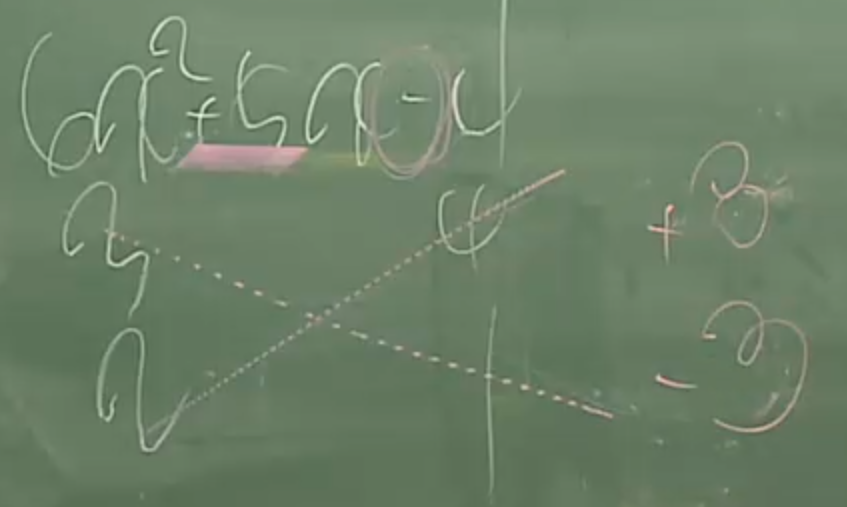| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 다이어트보조제 성분
- 킨즈 르베르 유모카
- 다이어트보조제 성분 정리
- 음악ai
- 기억의궁전
- 작문연습
- 킨즈 르베르 웨건
- 비스테로이드성 소염진통제
- 기술
- 아이디어
- 일일수학
- 수포자
- 사조영웅전2017
- 유투브
- 모티브
- ai기술
- 자면서공부하는법
- 연습또연습
- 로먼룸기억법
- 생성형AI
- 애드센스
- 사조영웅전2024 보러가기
- 수학개념
- 다시 시작
- AIVA
- 팻버닝
- Ai
- 다이어트 보조제
- 나이트버닝
- 잘할수있도록
- Today
- Total
득능막망-습득한 정보를 저장하자
2. 다항식(4)~(10) 기본개념의 변형개념 본문
1. 약수는 내용물 공약수는 공통된 내용물
(예: 54는 2 하나, 3 3개로 이뤄져있다. 18은 2 하나, 3 2개로 이뤄져있다.
그러면 공약수는 2 한개, 3 두개로 만들 수 있는 모든 수이고 최대공약수는 2*3^2이다.)

2. 배수는 어떤 수의 정수를 곱한것 공배수는 두 수의 내용물을 다 가지고 있는 수에 정수를 곱한것
(예: 54=2*3^3, 18=2*3^2일때 두 수의 공배수는 2*3^3에 정수를 곱한 것이고 최소공배수는 2*3^3 이다.)

3. 최대공약수는 G로 표기하고 최소공배수는 L로 표기한다.
4. 어떤수 A, B의 최대공약수가 G 이고 각각 남은 내용물이 a, b 라고 할 때
A=Ga, B=Gb, L=Gab, AB= G^2ab
(이는 Gab*G로 바꿀 수 있고 앞 식에 따라 AB=LG로 바꿀 수 있다.)라고 할 수 있다.

5. a+a=2a 이고 a*a=a^2 이다.
6. 분수/분수는 번분수라고 한다. 안에거 곱하면 분모, 바깥에거 곱하면 분자가 된다.
번분수에서는 분자끼리 약분이 가능하고 분모끼리도 약분이 가능하다.
7. 대입은 변수인 문자 위치에 정해진 값을 집어넣는 것이다.
(예: 5x+x^2의 식에서 x=-2일때 값은 5(-2)+(-2)^2 라고 쓸 수 있다.)
8. 항이란 +로 구분된 것.
(2+3-1은 3개의 항이고 각각 2,3,-1이다. -1은 2+3+(-1)로 표현하기 때문에 -도 같이 따라간다)
9. 항이 1개이면 단항식이고 1개 이상의 합으로 이뤄진 식을 다항식이라고 한다.(단 단항식도 다항식에 포함된다)
10. 상수항= 변수문자가 없이 숫자로만 이뤄진 항
11. 계수= 문자변수항 앞에 곱해진 값(문자 변수가 더해진 갯수, 5x=x+x+x+x+x이고 5가 계수임)
12. 차수= 문자변수가 곱해진 값(문자변수가 곱해진 갯수, x^5=x*x*x*x*x이고 5차항임)
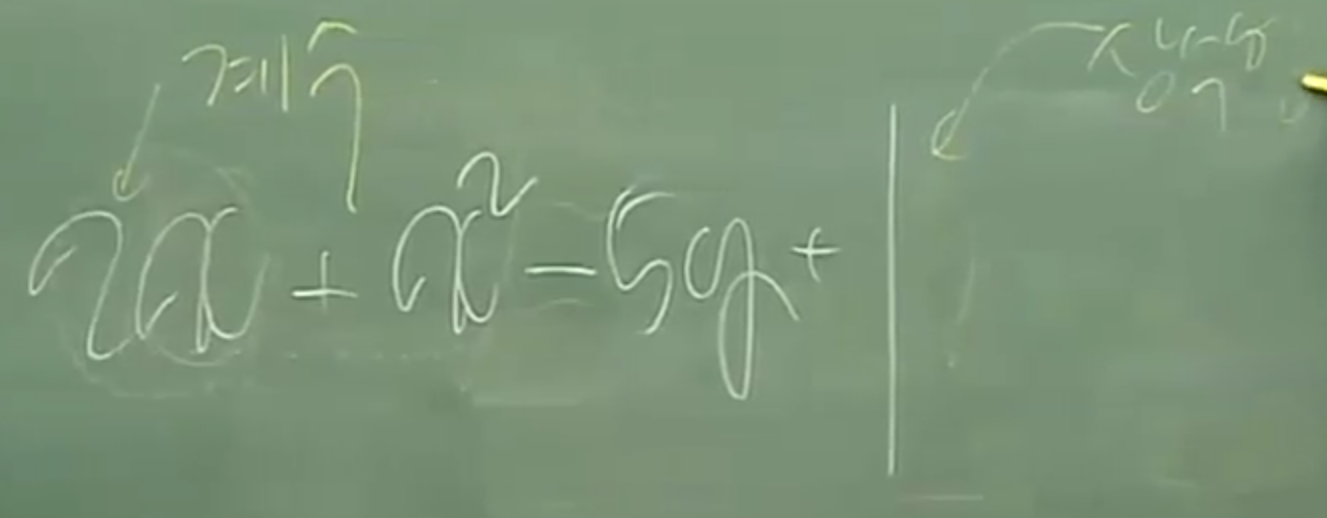
13. 수식을 정리할때는 차수가 높은 순서대로 정리한다.(내림차순)
14. 분배법칙은 계수를 괄호안의 모든 수와 곱하여 표시하는 것
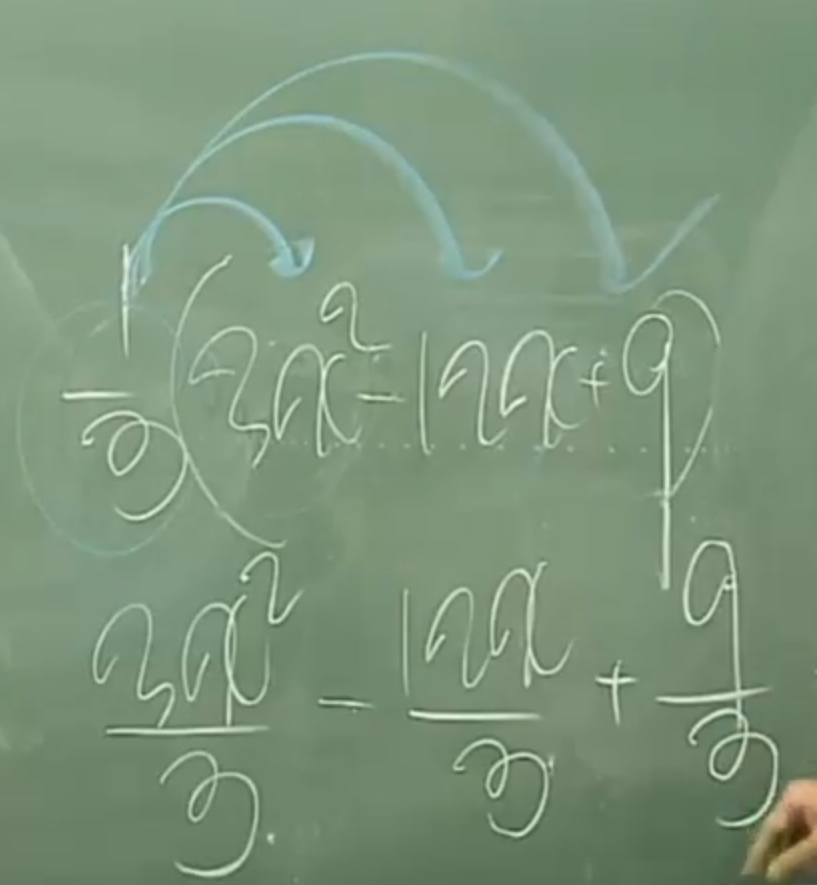
15. 동류항(종류가 똑같은 항)= 차수가 같은 항을 의미하고 상수항끼리는 동류항이다.
동류항 끼리는 계수를 더하거나 뺄 수 있다. (예: 2x+4-6x+8=-4x+12)
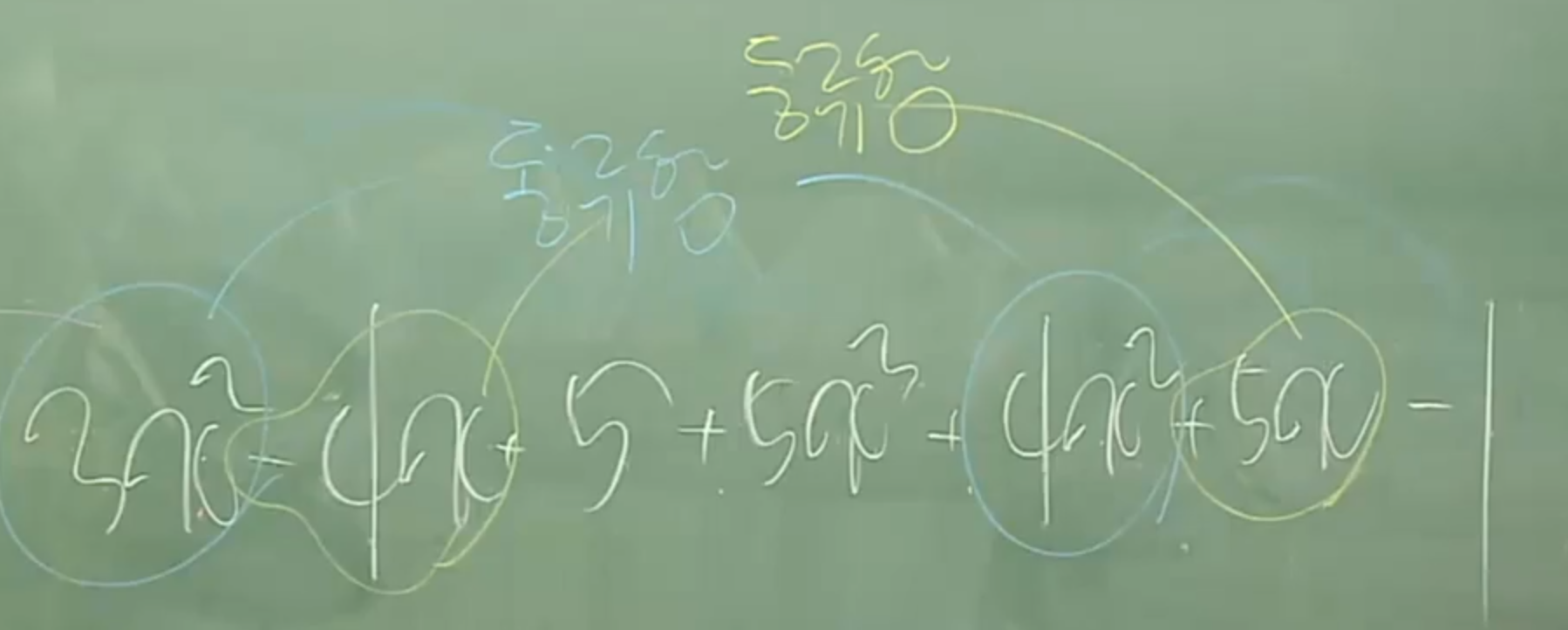
16. 괄호가 여러종류일때는 소()->중{}->대[] 순으로 괄호를 푼다.
17. a^3일때 a는 밑이라고 하고 3는 지수라고 한다. 이는 a*a*a이다.
18. a^3*a^2은 풀어쓰면 a*a*a*a*a이므로 a^5이다.
따라서 밑이 같은 수를 곱했을 때 지수는 더하면 된다.(지수법칙1)
19. a^3/a^2는 풀어쓰면 a*a*a/a*a로 약분되어 a와 같다.
따라서 밑이 같은 수를 나눌 때 지수는 빼면 된다.(지수법칙2)
20. (a^3)^2은 풀면 (a^3)*( a^3)이므로 a^6과 같다.
따라서 (a^지수1)^지수2는 a^(지수1*지수2)와 같고 지수1,2의 자리도 바꿀 수 있다. (지수법칙3)
21. (ab)^3=a^3b^3(=ab*ab*ab) 이고(b/a)^3=b^3/a^3(= b/a* b/a* b/a)이다 (지수법칙4)
(=곱꼴이나 분수꼴의 지수는 각각 지수)
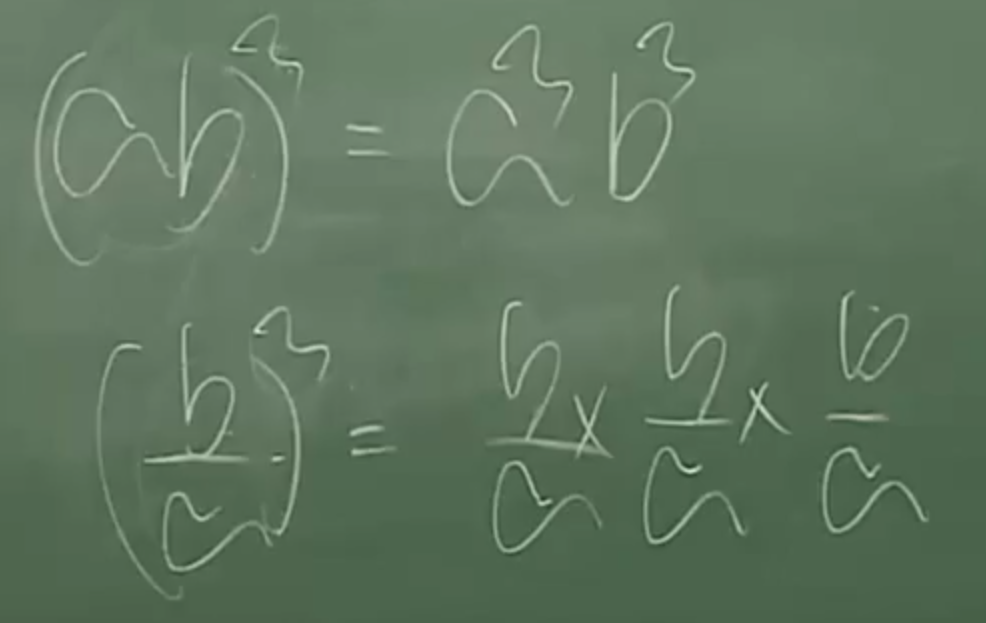
22. 2의 거듭제곱수= 2(2^1), 4, 8, 16, 32, 64, 128, 256, 512, 1024(2^10) 정도는 외우기
23. 3의 거듭제곱수= 3(3^1), 9, 27, 81, 243(3^5) 정도는 외우기
24. 모든수의 ^0은 1이다. 나중에 i라는 허수가 나오는데(1+ i)^0도 1이다. (단 0^0은 정의하지 않는다.없다.)
25. 다항식의 경우 괄호를 풀고 동류항끼리 계산하여 간단히 할 수 있다.(몇 차식인지 상관 없음)
(빼기가 괄호앞에 있을 경우는 주의할 것->괄호 안에 있는 부호를 다 반대로 바꿔야함)
26. 완전제곱식 (a+b)^2= (a+b)(a+b)이므로 a^2+ab+ab+b^2= a^2+2ab+b^2가 된다.
(예: 101^2=(100+1)^2)
27. 완전제곱식 (a-b)^2= (a-b)(a-b)이므로 a^2-ab-ab+b^2= a^2-2ab+b^2가 된다.
(예: 99^2=(100-1)^2)
(따라서 완전제곱식은 앞에거 제곱 두배에 앞뒤하고 뒤에거 제곱. -는 포함해서 앞에거든 뒤에거든 한다.)
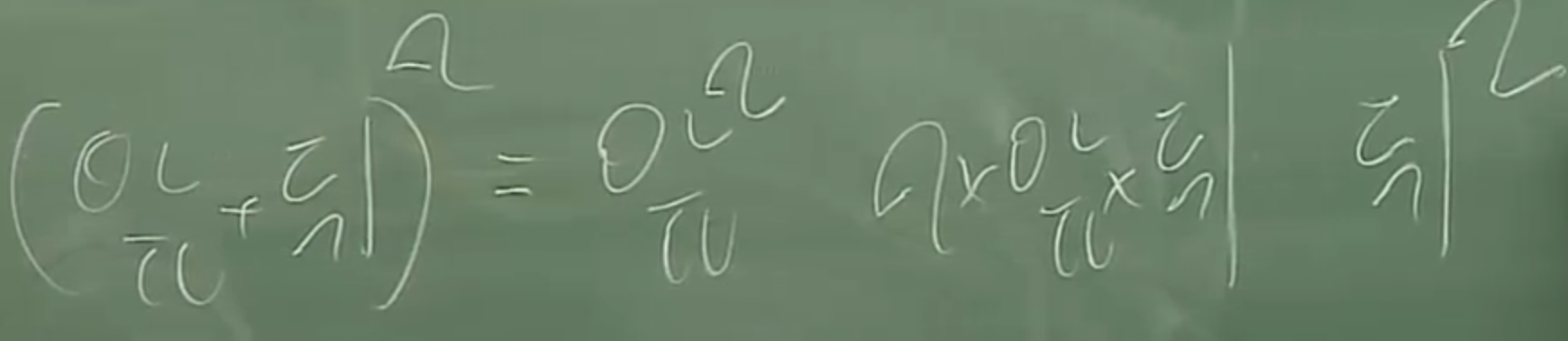
28. 합과차 공식 (a+b)(a-b)= a^2+ab-ab-b^2= a^2-b^2
(따라서 앞에거 제곱 빼기 뒤에거 제곱)
(예:101*99=(100+1)(100-1)

29. (x+a)(x+b)=x^2+ax+bx+ab=x^2+(a+b)x+ab(합과곱 공식. 주의할 부분 좌변 1차항 x의 계수가 1이어야함)
30. 29번에서 좌변 x의 계수가 1이 아닌경우는 그냥 전개해서 계산한다.
(예: (ax+b)(cx+d)=ac(x^2)+(ac+bd+)x+bd)
31. 완전제곱식의 변형은 (a+b)^2= a^2+2ab+b^2를 (a+b)^2- 2ab = a^2+b^2로 바꿀 수 있다.(제곱의 합공식)
(제곱의 합= 합의 제곱 - 곱의 두배)
(제곱의 합은 합과 곱의 값이 있으면 구할 수 있다.)
(단, 27번의 완전제곱식(a-b)^2의 변형으로 차와 곱의 값이 있어도 구할 수 있다.)
(따라서 제곱의 합과 합의 값이 있으면 두 수의 곱의 값을 구할 수 있다.)
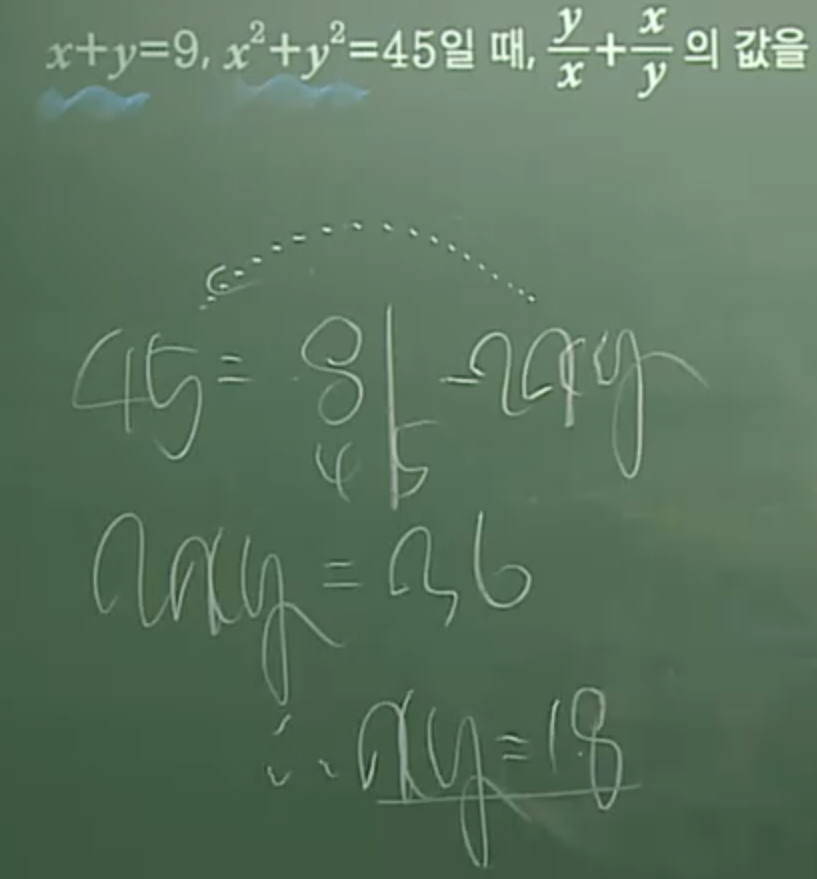
32. (x-3)(x+1)=x^2-2x-3일때 왼쪽식에서 오른쪽으로 가는 방법을 전개라하고 반대는 인수분해라고 한다.
단항식을 다항식으로 바꾸면 전개, 다항식을 단항식으로 바꾸면 인수분해
따라서 전개와 인수분해는 역과정이다.(미분과 적분도 역과정)
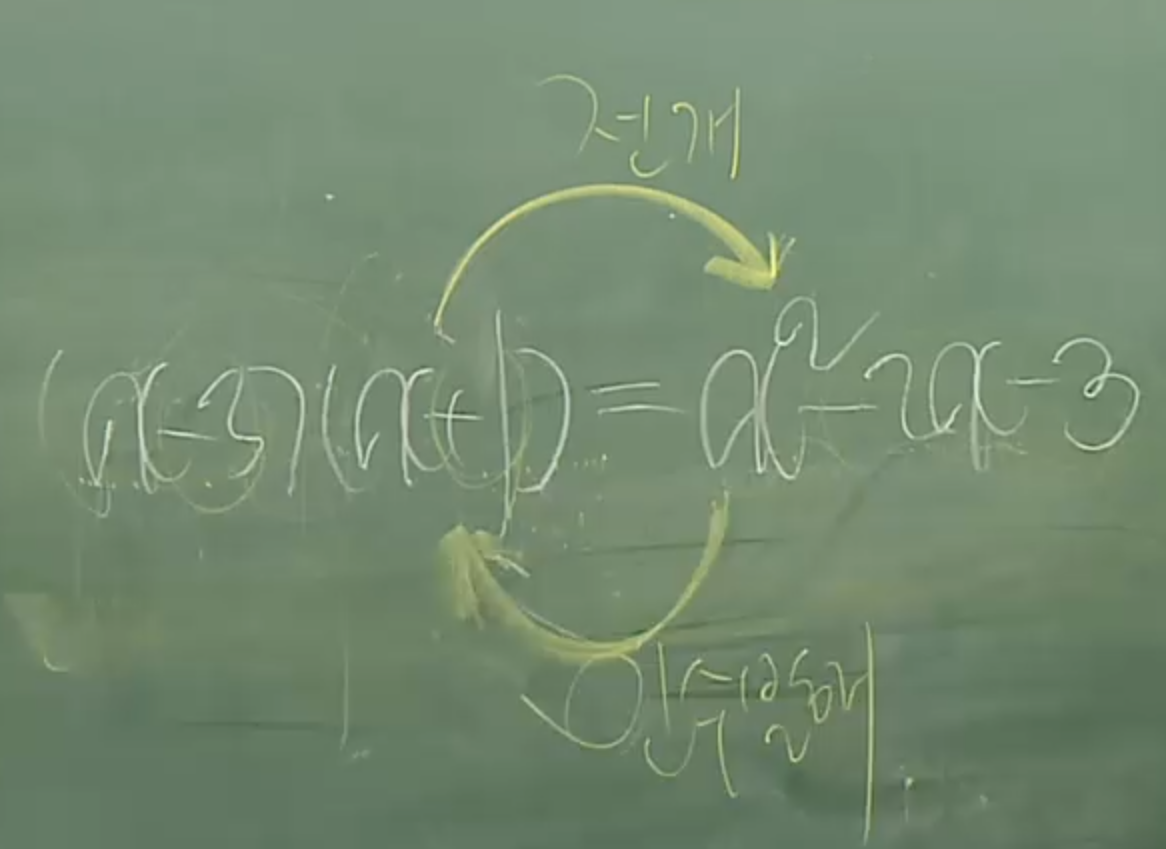
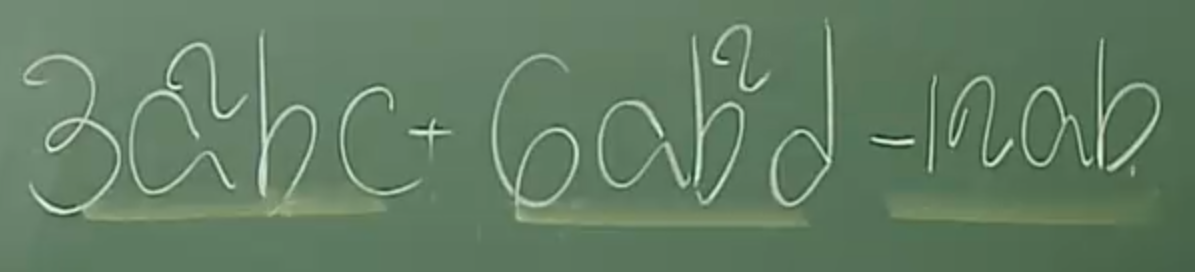
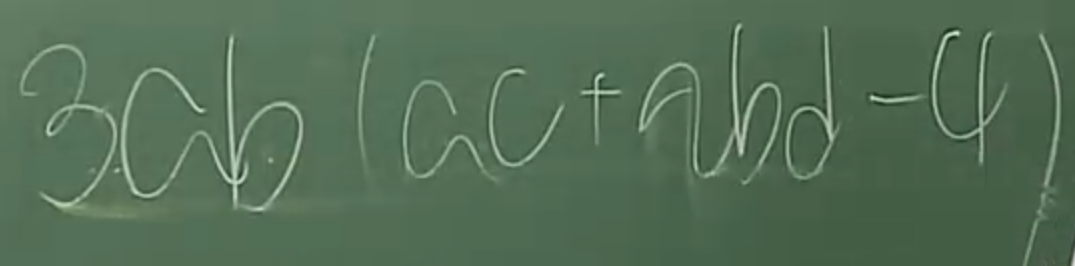
33. 맨 앞의 항과 맨 뒤의 항이 제곱으로 이뤄졌다면 완전제곱식으로 변형이 가능할지도 모른다.(가설수립)
그리고 완전제곱식으로 변형한 다음 수립한 가설을 확인하면 된다.(다시 전개해봄)
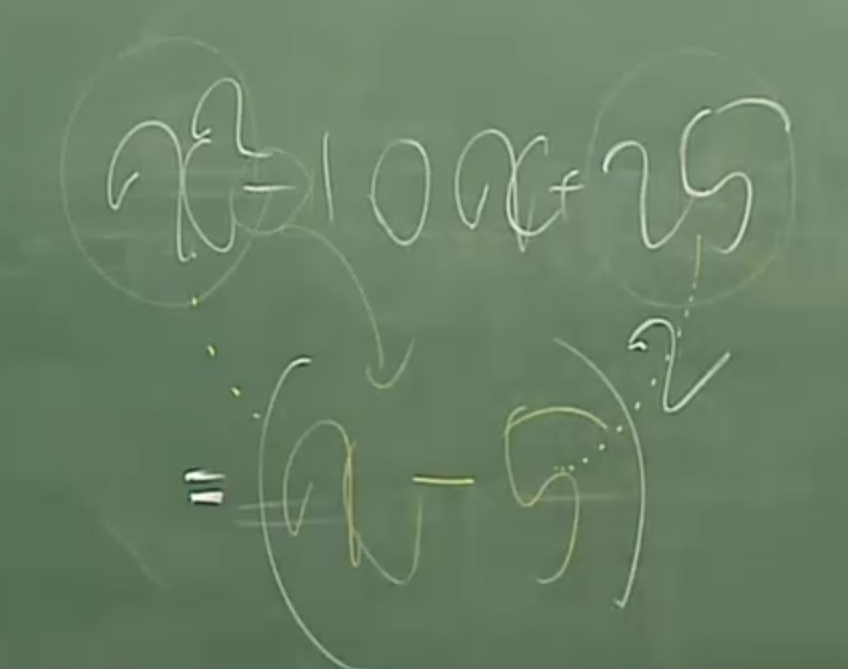
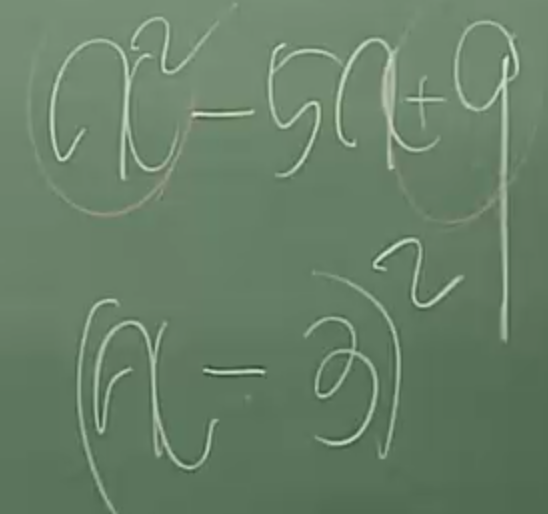
34. 이차항의 계수가 1인경우에만 일차항의 계수의 반의제곱을 하면 전개식 상의 상수값을 구할 수 있다.
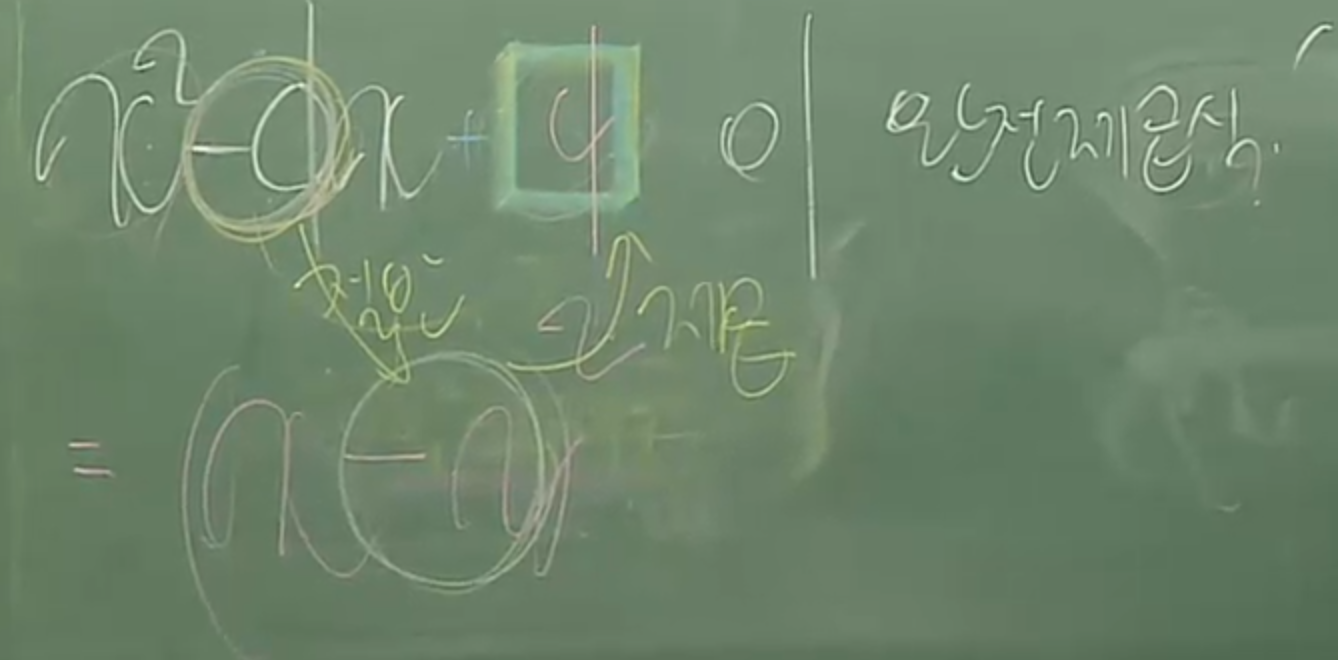
35. 34번을 반대로 하여 상수값이 있을 때 일차항의 계수는 상수에 루트하고 두배 하면된다.
(단, 일차항의 계수가 +,-둘다 완전제곱식이 되므로 일차항의 계수를 구하는 문제의 답은 +-계수값이 된다.)
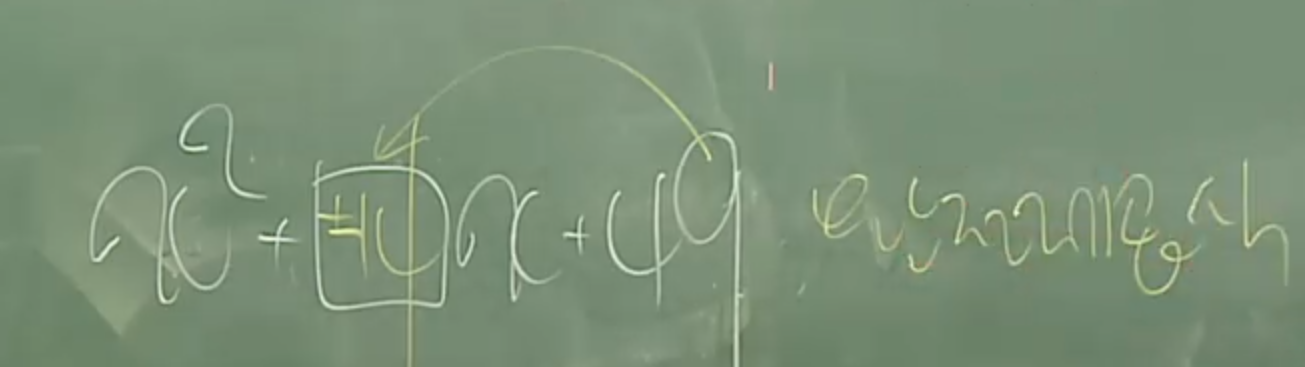
36. a^2-b^2 형태는 28번에 따라서 (a+b)(a-b)로 바꿀 수 있다.
37. 제곱이 있는 식을 인수분해 할 때는 지수가 남아있을 경우 인수분해가 더 되는지 반드시 확인한다.
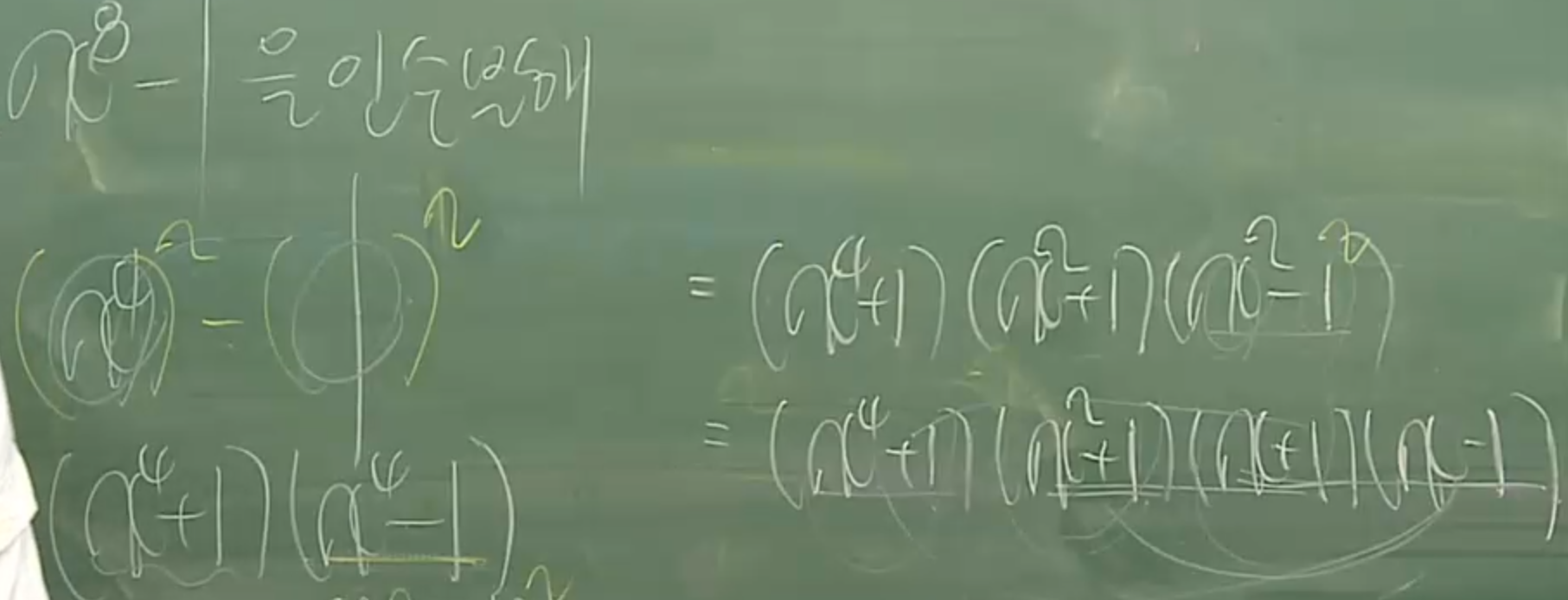
38. 이차항의 계수가 1이고 일차항이 +인경우의 인수분해는 곱해서 상수값이 되는수와 더해서
일차항의 계수가 되는 값을 비교하여 인수분해할 수 있다.
(이때 상수값의 부호는 두수의 부호가 같은지 다른지를 알려준다.)
결론1. 최고차항의 계수가 1인 이차식의 인수분해를 할때는 상수의 부호를 확인한다.
(상수의 부호가+면 두 수의 부호가 같고 -면 두수의 부호가 다르다는 것을 의미함.
왜? 28번 29번을 거꾸로 돌려보면됨)
결론2. 곱해서 상수의 절대값이 되는 두 수를 나열한다.
결론3. 나열한 수에서 합이 일차항의 계수가 되는 값을 찾는다.
결론4. 두 수에 변수항을 붙여준다.
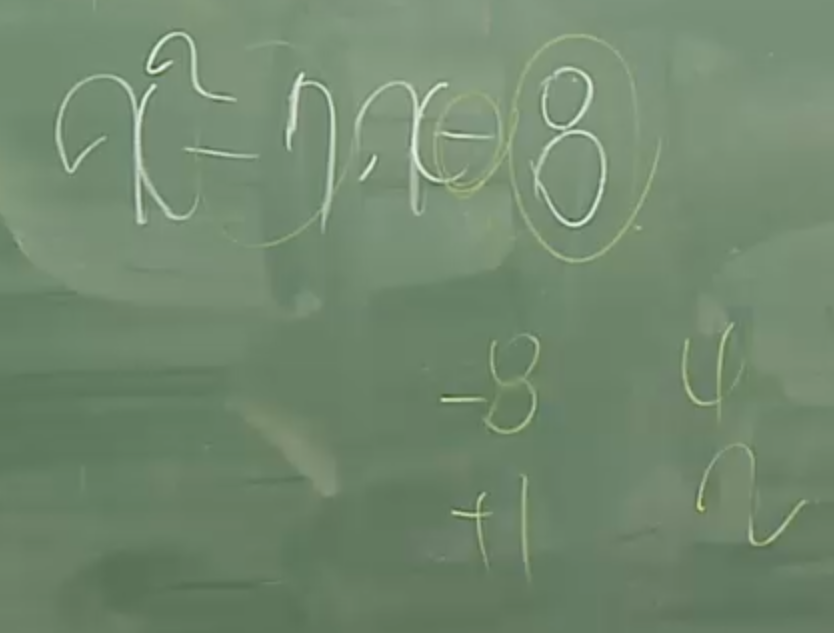
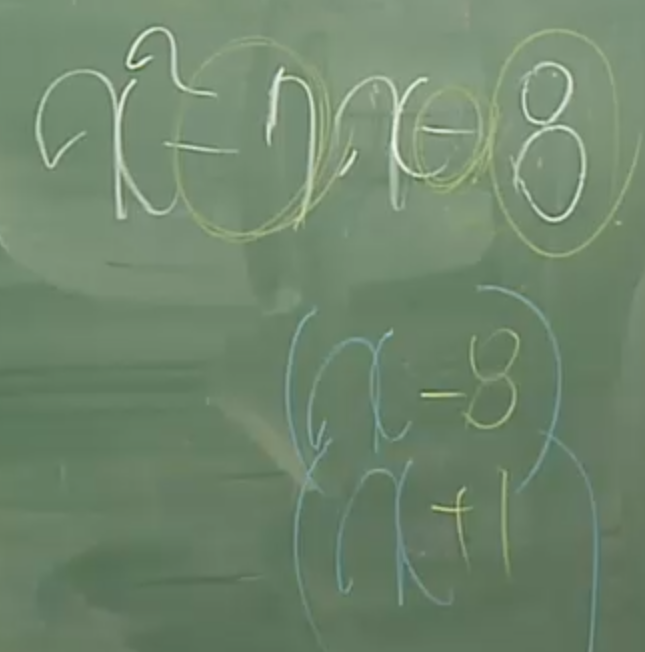
39. 최고차항의 계수가 1이 아닌경우 시행착오를 거듭하여 풀어야 한다.(나중에 빨라짐)
(38번을 최고차항과 상수에 각각 적용해야 한다.)
(이때도 상수값의 부호가 의미하는 것은 동일함. 양수면 두식의 부호가 같고 음수면 두식의 부호가 다름)